Límites: una introducción para jóvenes aspirantes a matemáticos

Introducción
Los límites son una herramienta básica y esencial en matemáticas. Se utilizan de una u otra forma en casi todas las ramas de las matemáticas, y además representan una de las primeras dificultades a las que uno se enfrenta cuando empieza a estudiar matemáticas. Esto se debe a que suele ser la primera vez que uno ve una definición formal de un concepto matemático, lo que es realmente un reto para la mayoría de estudiantes, como lo fue para mí. La dichosa definición de límite es la siguiente:
Dada una sucesión de números reales, \(\{x_n\}_{n\in\mathbb{N}}\subset\mathbb{R}\), se dice que el número real \(L\) es el límite de la sucesión, \[L=\lim_{n\rightarrow\infty}x_n\] si \[\forall\varepsilon>0,\exists N\in\mathbb{N} | \forall n\geq N, |x_n-L|<\varepsilon.\]
Explicación intuitiva de la definición
Vamos a ir paso a paso. Primero, veamos qué es una sucesión de números reales, \(\{x_n\}_{n\in\mathbb{N}}\subset\mathbb{R}\).
Sucesiones
Siempre que vemos los símbolos \(\{\}\), estamos indicando que hablamos de un conjunto. Lo que haya entre los corchetes es lo que forma el conjunto. Hay varias maneras de definir un conjunto. Por ejemplo, podemos definir un conjunto enumerando todos sus elementos:
El conjunto de los números de un dado es \(\{1,2,3,4,5,6\}\).
Otra manera es indicando una propiedad que cumplen los elementos del conjunto:
El conjunto de los números pares es \(\{x\in\mathbb{N} | x\text{ es par}\}\).
Aquí, \(\mathbb{N}\) es el conjunto de los números naturales, \(\mathbb{N}=\{1,2,3,4,5,\dots\}\). La barra vertical \(|\) se lee “tal que” y el símbolo \(\in\) se lee “pertenece a”. Por tanto, la definición anterior se lee “el conjunto de los números \(x\) que pertenecen a los naturales y son pares”. Es importante darse cuenta que esta segunda forma de definir conjuntos es comúnmente más útil que la primera, ya que resulta complicado enumerar todos los elementos de un conjunto infinito.
Por otro lado, \(\mathbb{R}\) es el conjunto de los números reales, que incluye a los números naturales, enteros (los naturales, los negativos y el 0), los racionales (los que se pueden escribir como una fracción) y los irracionales (los que no se pueden escribir como una fracción, como \(\pi\) o \(\sqrt{2}\)).
\(\subset\) significa “subconjunto de”. Por ejemplo, \(\{1,2,3\}\subset\{1,2,3,4,5\}\), pero \(\{1,2,3,4,5\}\not\subset\{1,2,3\}\). Por tanto, en nuestra definición de sucesión, estamos diciendo que \(\{x_n\}\subset\mathbb{R}\), es decir, que los elementos de la sucesión son números reales.
Finalmente, cuando utilizamos un subíndice, como la \(n\) en \(x_n\), estamos indicando que estamos hablando de un elemento concreto de la sucesión. Por ejemplo, \(x_1\) es el primer elemento de la sucesión, \(x_2\) es el segundo, y así sucesivamente. Por tanto, \(\{x_n\}_{n\in\mathbb{N}}\subset\mathbb{R}\) significa:
“Un conjunto de números reales \(x_n\), enumerados por un índice \(n\) que pertenece a los naturales”.
Algunos ejemplos de sucesiones pueden ser:
- La sucesión de los números naturales:
\(\{x_n | x_n=n, n\in\mathbb{N}\}\)
- La sucesión de los números pares:
\(\{x_n | x_n=2n, n\in\mathbb{N}\}\)
- La sucesión de los números impares:
\(\{x_n | x_n=2n+1, n\in\mathbb{N}\}\)
- La sucesión de los inversos de los números naturales:
\(\{x_n | x_n=\frac{1}{n}, n\in\mathbb{N}\}\)
Observa cómo el índice puede utilizarse para definir el elemento correspondiente en la sucesión. Esto es muy útil, ya que podemos definir de manera precisa la relación entre los índices y los elementos de la sucesión.
Límites
Ahora que sabemos qué es una sucesión, vamos a ver qué significa que un número real \(L\) sea el límite de la sucesión. Para ello, vamos a utilizar la definición de límite que hemos visto antes:
\(L\) es el límite de la sucesión \(\{x_n\}_{n\in\mathbb{N}}\) si \(\forall\varepsilon>0,\exists N\in\mathbb{N} | \forall n\geq N, |x_n-L|<\varepsilon.\)
\(L\) es simplemente un número real, que representa el límite de la sucesión.
Pasemos a la parte jugosa de la definición: \(\forall\) se lee “para todo”, y es muy importante entenderlo bien. Voy a intentar poner un ejemplo para aclarar su significado. Imagina que tienes la siguiente afirmación:
Para todo número real \(x\), \(x^2\geq0\).
Esto solo es cierto, si funciona para todos los números reales. En efecto, al multiplicar todo número real por sí mismo, obtenemos un número positivo o cero. Por tanto, la afirmación anterior es cierta. Sin embargo, si la afirmación fuera:
Para todo número real \(x\), \(x^2>0\).
Entonces la afirmación sería falsa, ya que si \(x=0\), \(x^2=0\), y por tanto no se cumple que \(x^2\ge0\). Basta con que un único número real no cumpla la afirmación para que esta sea falsa. Por tanto, \(\forall\) significa que la afirmación debe ser cierta para todos los elementos del conjunto que estamos considerando.
Es decir, que al decir \(\forall\varepsilon>0\), estamos diciendo que la afirmación que viene a continuación debe ser cierta para todos los números reales positivos.
Por otro lado, \(\exists\) se lee “existe”, y significa que debe existir al menos un elemento del conjunto que cumpla la afirmación. Por ejemplo, la afirmación:
Existe un número real \(x\) tal que \(x^2=2\).
Es cierta, ya que \(x=\sqrt{2}\) cumple la afirmación. Sin embargo, la afirmación:
Existe un número real \(x\) tal que \(x^2=-1\).
Es falsa, ya que no existe ningún número real que cumpla la afirmación. Por tanto, \(\exists\) significa que la afirmación debe ser cierta para al menos un elemento del conjunto que estamos considerando.
Por tanto, al decir \(\exists N\in\mathbb{N}\), estamos diciendo que la afirmación que viene a continuación debe ser cierta para al menos un número natural.
Combinemos ahora \(\forall\) y \(\exists\). La afirmación:
\(\forall\varepsilon>0,\exists N\in\mathbb{N}\)
Significa que para todo número real positivo \(\varepsilon\), existe al menos un número natural \(N\) que cumple la afirmación que viene a continuación. Vamos a poner un ejemplo previo a la definición de límite para aclarar esto:
\(\forall\varepsilon>0,\exists N\in\mathbb{N} | N>\varepsilon\)
Esta afirmación es cierta e interesante. Lo que quiere decir es: Si elegimos un número real positivo cualquiera, \(\varepsilon\), siempre podemos encontrar un número natural \(N\) que sea mayor que \(\varepsilon\). Esto es cierto, ya que los naturales son infinitos, y por tanto siempre podemos encontrar uno mayor que cualquier número real positivo. Por ejemplo, si \(\varepsilon=\pi\), podemos elegir \(N=4\), ya que \(4>\pi\). Si \(\varepsilon=1\), podemos elegir \(N=2\), ya que \(2>1\). Si \(\varepsilon={\pi^\pi}^{14}\), podemos elegir \(N={4^4}^{14}\), ya que \({4^4}^{14}>{\pi^\pi}^{14}\). Y así podríamos hacer con cualquier número que podamos pensar.
Es decir, que de una forma más intuitiva, podemos reformular \(\forall\varepsilon>0,\exists N\in\mathbb{N}\) como:
Si elegimos un número real positivo cualquiera, \(\varepsilon\), siempre podemos encontrar un número natural \(N\) de tal manera que…
Ahora, vamos a ver qué significa el resto de la definición de límite:
\(\forall\varepsilon>0,\exists N\in\mathbb{N} | \forall n\geq N, |x_n-L|<\varepsilon\)
Vemos que encontramos de nuevo un \(\forall\), esta vez refiriendose a \(n\). Es decir, que la afirmación que viene a continuación debe ser cierta para todos los elementos de la sucesión que sean mayores o iguales que \(N\).
Finalmente, vemos que aparece \(|x_n-L|<\varepsilon\). Esto significa que la distancia entre \(x_n\) y \(L\) debe ser menor que \(\varepsilon\).
Es decir, la definición de límite se puede reformular como:
Si elegimos un número real positivo cualquiera, \(\varepsilon\), siempre podemos encontrar un índice de la sucesión, \(N\), de tal manera que, para todos los elementos de la sucesión a partir de este índice, la distancia entre el elemento y el límite sea menor que \(\varepsilon\).
Ejemplos
Vamos, por último, a usar algunos ejemplos para terminar de aclarar la definición de límite.
Tomemos la sucesión de los inversos de los números naturales, que vimos antes:
\(\{x_n | x_n=\frac{1}{n}, n\in\mathbb{N}\}\)
Esta sucesión se ve así:
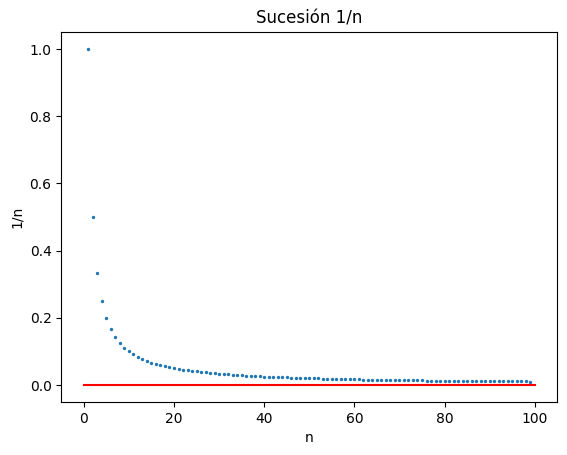
Intuitivamente, podemos darnos cuenta de que el límite de esta sucesión es 0. Esto es así porque, a medida que \(n\) crece, \(\frac{1}{n}\) se hace más y más pequeño, y por tanto se acerca a 0. Vamos a intentar ver esto con la definición que hemos visto. Es decir, tomamos \(L=0\), y vamos a ver si cumple la definición de límite.
Comencemos, como hemos visto antes, eligiendo un número real positivo: \(\varepsilon=0.1\). Ahora, tenemos que encontrar un índice de la sucesión, \(N\), de tal forma que todos los elementos posteriores a \(x_N\) estén a una distancia menor que \(\varepsilon\) de \(L\). Es decir, que \(|x_n-L|<0.1\) para todo \(n\geq N\). Vamos a ver si podemos encontrar un \(N\) que cumpla esto:
- N=1: \(|x_1-L|=|1-0|=1>0.1\)
- N=2: \(|x_2-L|=|0.5-0|=0.5>0.1\)
- N=3: \(|x_3-L|=|0.33-0|=0.33>0.1\)
- N=4: \(|x_4-L|=|0.25-0|=0.25>0.1\)
- …
- N=10: \(|x_10-L|=|0.1-0|=0.1=0.1\)
- N=11: \(|x_11-L|=|0.09-0|=0.091<0.1\)
- N=12: \(|x_12-L|=|0.083-0|=0.083<0.1\)
Y la cantidad continúa disminuyendo a medida que \(n\) crece. Por tanto, podemos ver que, para \(N=11\), se cumple que \(|x_n-L|<0.1\) para todo \(n\geq N\). Es decir, que para \(\varepsilon=0.1\), podemos encontrar el índice adecuado. En la siguiente imagen se puede ver esto gráficamente:
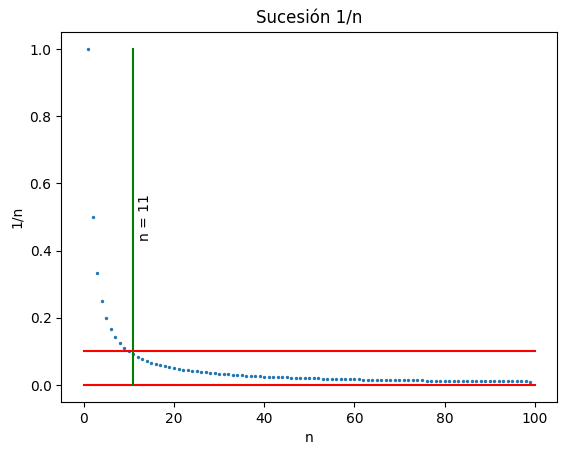
Ahora bien, esto todavía no significa que \(L=0\) sea el límite de la sucesión. Solo lo hemos comprobado para un valor de \(\varepsilon\). Sin embargo, el \(\forall\) nos obliga a comprobarlo para todos los posibles valores de \(\varepsilon\)!
Está claro que comprobar todos los valores, uno a uno, es imposible, ya que podemos tomar \(\varepsilon\) tan pequeños como queramos. Por tanto, tenemos que encontrar una manera de comprobarlo para todos los valores de \(\varepsilon\) de una vez.
Para hacer esto, tomemos un \(\varepsilon\) cualquiera, general. Este puede ser tan pequeño o tan grande como queramos. Ahora bien, una cosa que podemos hacer es tomar \(y=\frac{1}{\varepsilon}\), que también es un número real. Antes vimos una propiedad interesante: dado un número real cualquiera, siempre podemos encontrar un número natural mayor que este. Por tanto, hay un número natural \(N\) tal que \(N>y=\frac{1}{\varepsilon}\).
Esta claro, además, que si tomamos otro natural \(n>N\), este también verifica \(n>y=\frac{1}{\varepsilon}\). Por tanto, si tomamos el inverso, vemos que \(\frac{1}{n}<\varepsilon\). Es decir, que para cualquier \(\varepsilon\) que tomemos, siempre podemos encontrar un \(N\) tal que \(\frac{1}{n}<\varepsilon\) para todo \(n>N\). Esto es exactamente lo que necesitamos para que \(L=0\) sea el límite de la sucesión.
¡Ahora sí! Podemos asegurar con completa seguridad que \(0=\lim_{n\rightarrow\infty}\frac{1}{n}\). Es decir, que el límite de la sucesión de los inversos de los números naturales es 0.
Aplicaciones de los límites
Los límites son super importantes, tanto en matemáticas en general, como en muchos aspectos prácticos. Te voy a poner algunos ejemplos que espero que te convenzan de leer varias veces lo que he explicado, hasta que lo entiendas bien:
1- La definición de límite es la primera gran barrera a la que te enfrentarás en la carrera de matemáticas. Estoy convencido de que muchas de las personas que no consiguen terminar la carrera de matemáticas, es porque no consiguieron entender bien la definición de límite. Por tanto, si quieres ser matemático, tienes que hacer un esfuerzo por entenderla.
2- Los límites son la base del cálculo. Proporcionan la base para definir las derivadas y las integrales, que son dos de los conceptos más importantes en matemáticas. Sin los límites, no podríamos definir estas dos herramientas tan importantes. Pero además se utilizan en topología, probabilidad, estadística, análisis numérico, etc. Más aún, los límites son en muchas ocasiones el puente de unión entre dos ramas de las matemáticas. Por ejemplo, el análisis funcional surge de la unión del análisis real y el álgebra lineal, y los límites son la herramienta que permite unir estas dos ramas.
3- La inteligencia artificial se basa en gran medida en el concepto de derivada, que a su vez se basa en el concepto de límite. En mi experiencia, entender bien estos conceptos matemáticos me ha dado una gran ventaja a la hora de entender los conceptos de inteligencia artificial, por qué funcionan y cómo funcionan. Otros compañeros que no tenían una base sólida en matemáticas, han encontrado más dificultades para trabajar con estos conceptos.
4- Es un concepto bonito. Todos los matemáticos recuerdan esta definición, no porque la sepan de memoria, sino porque la han interiorizado. La hemos utilizado tantas veces, en tantos contextos diferentes, que la tenemos grabada en la cabeza. Es una definición que te hace pensar, que te hace reflexionar, que te hace entender el mundo de una manera diferente. Es una definición que te hace mejor persona. Y no lo digo en broma. Es la puerta de entrada a la lógica matemática, donde la mente se abre y se expande, y donde se aprende a pensar de una manera diferente.
Espero que este artículo te haya ayudado a entender mejor los límites. Si tienes cualquier duda, no dudes en contactar conmigo. ¡Hasta la próxima!