Superficies de Willmore

Introducción

Hice mi Trabajo de Fin de Grado en Matemáticas sobre Superficies de Willmore. Intentaré explicar las ideas principales de la tesis en este post.

En primer lugar, veremos un poco de historia de estas superficies. En segundo lugar, explicaré qué es el funcional de Willmore, \(W\). Luego, visitaré algunos de los resultados más importantes sobre superficies de Willmore. Finalmente, explicaré los principales resultados de mi tesis, que son la invarianza del funcional de Willmore bajo transformaciones conformes del espacio y la derivación de la primera variación del funcional de Willmore, utilizando herramientas básicas de geometría diferencial en el espacio euclidiano tridimensional, \(\mathbb{R}^3\).

Si está interesado en el tema, puede leer el trabajo completo, su presentación o poster.

Historia

Las superficies de Willmore han sido un tema de gran interés desde su creación en 1965, cuando Willmore publicó su influyente artículo Note on embedded surfaces ¹. Definió un funcional, más tarde llamado como él, dado por \[\tau(S)=\frac{1}{2\pi}\int_{S}H^2dS\], donde \(S\) es una superficie regular cerrada orientable del espacio euclídeo y \(dS\) su elemento de área, con \(H\) denotando la curvatura media de \(S\). Willmore pretendía encontrar la relación entre este funcional y la característica de Euler, \(\mathcal X(S)\), esperando descubrir una relación similar al teorema de Gauss-Bonnet. Aunque no se estableció tal relación, Willmore logró extraer propiedades de \(\tau(S)\) conociendo el valor de \(\mathcal X(S)\). Por ejemplo, demostró que para una esfera de radio \(r>0\), \[\tau(\mathbb{S}^2(r))=2\], que es el ínfimo (y mínimo) de \(\tau\) para todas las superficies posibles \(S\).

Desde entonces, el funcional se define normalmente como \[W(S) = \int_{S}H^2dS\], multiplicando el funcional original de Willmore por \(2\pi\). El estudio de ambos funcionales es equivalente cuando se trata de encontrar superficies que los minimicen. Otra definición alternativa es \[W(S) = \int_{S}(H^2-K)dS\], donde \(K\) es la curvatura gaussiana de la superficie en cada punto. Este funcional también es equivalente a los anteriores, ya que el teorema de Gauss-Bonnet implica que sólo se está añadiendo un término constante. Después de encontrar el mínimo absoluto de \(W\), Willmore intentó alcanzar un resultado similar para superficies con característica de Euler \(\mathcal{X}(S)=0\), las superficies homeomorfas a un toro. Aunque no lo consiguió, caracterizó el mínimo de \(\tau\) entre todos los toros de revolución, dando lugar a lo que se conoció como la conjetura de Willmore. Esta conjetura fue finalmente demostrada por Marques y Neves en 2014, casi 50 años después de que se formulara por primera vez ².

El funcional de Willmore

El funcional de Willmore de una superficie orientable, compacta y regular, \(S\), se define como: \[\int_S H^2 dS,\] donde \(H\) es la curvatura media de \(S\) y \(dS\) es el elemento de área de \(S\).

Entonces, definimos una superficie de Willmore como una superficie que es un punto crítico del funcional de Willmore.

The first interesting result that we can get is the following Theorem:

El primer resultado interesante que podemos obtener es el siguiente Teorema:

Teorema 1. Si \(S\) es una superficie orientable, compacta y regular, entonces \[W(S)\geq4\pi,\] con igualdad si y sólo si \(S\) es una esfera.

Podemos esbozar³ la demostración de este teorema de la siguiente manera:

Primero, \[W(S)=\int_S H^2 dS\geq\int_{S^+} H^2 dS,\] donde \(S^+\) es la parte de \(S\) donde \(K\) es positiva. Entonces, es bien sabido que \[H^2-K=\frac{(k_1-k_2)^2}{4}\geq0,\] donde \(k_1\) y \(k_2\) son las curvaturas principales de \(S\). Esto implica que \(H^2\geq K\). Ahora, podemos combinar las dos desigualdades anteriores para obtener \[W(S)\geq\int_{S^+} K dS=\text{area}(N(S^+)),\] donde \(N(\cdot)\) es la aplicación de Gauss de \(S\). Como \(S\) es compacta, se puede demostrar que \(N(S^+)\) es sobreyectiva. Por lo tanto \[W(S)\geq\text{area}(N(S^+))\geq\text{area}(\mathbb{S}^2)=4\pi.\] La igualdad se cumple si y sólo si \(H^2=K\), lo que implica que \(k_1=k_2\), es decir, \(S\) es una esfera, ya que es la única superficie con curvaturas principales constantes que es compacta.

Como Willmore estaba interesado en la relación entre la característica de Euler y el funcional de Willmore, exploró el comportamiento del funcional con diferentes familias de superficies. Por ejemplo, se puede demostrar que, para el toro de revolución con radio interior \(r\) y radio exterior \(R\), el funcional de Willmore está dado por \[W(\mathbb{T}(r,R))=\frac{\pi^2}{a\sqrt{1-a^2}},\] donde \(a=\frac{r}{R}\). Esto implica que el mínimo del funcional es \(2\pi^2\) y se alcanza cuando \(a=\frac{1}{\sqrt{2}}\), es decir, cuando \(R=\sqrt{2}\cdot r\).

La conjectura de Willmore

Tras encontrar el mínimo del funcional de Willmore entre todos los toros de revolución, Willmore también estudió una familia más general de toros: los toros generalizados. Estas son superficies que se obtienen tomando un tubo alrededor de una curva cerrada en \(\mathbb{R}^3\). Los toros generalizados son superficies homeomorfas a un toro.

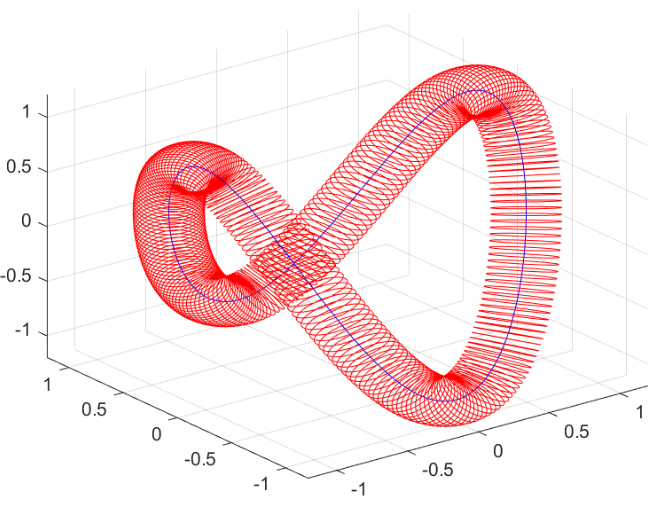
Demostró que el funcional de Willmore de cualquier toro generalizado es al menos \(2\pi^2\). Esto lo llevó a conjeturar que el mínimo del funcional de Willmore entre todas las superficies con característica de Euler \(\mathcal{X}(S)=0\) es \(2\pi^2\). Esto es conocido como la conjectura de Willmore:

Conjetura de Willmore (1965). Si \(S\) es una superficie orientable, compacta y regular con característica de Euler \(\mathcal{X}(S)=0\) (equivalentemente, su género es \(g(S)=1\)), entonces \[W(S)\geq2\pi^2,\] con igualdad si y sólo si \(S\) es un toro de revolución con radio interior \(r\) y radio exterior \(R=\sqrt{2}\cdot r\).

La demostración de este resultado evadió a los matemáticos hasta el 2014, cuando Marques y Neves lo probaron² usando técnicas avanzadas de la teoría geométrica de la medida.

Invarianza conforme del funcional de Willmore

Sean \(W_1,W_3\) conjuntos abiertos y conexos del espacio euclídeo. Entonces, una transformación conforme es una función \(\Phi:W_1\to W_2\) si, para todo \(p\in W_1\), \(d\Phi_p\) es una aplicación lineal conforme. Más concretamente, esto significa que existe una función diferenciable \(\lambda:W_1\to\mathbb{R}\setminus\{0\}\) tal que \[\left\langle d\Phi_p(v),d\Phi_p(w)\right\rangle=\lambda(p)^2\left\langle v,w\right\rangle,\] para todo \(v,w\in\mathbb{R}^3\) y \(p\in W_1\). La función \(\lambda\) se llama el factor conforme de \(\Phi\).

Se puede demostrar que esta definición es equivalente a decir que una transformación conforme es una función que preserva los ángulos entre curvas.

El teorema de Liouville⁴ establece que toda transformación conforme inyectiva entre dos conjuntos abiertos y conexos en \(\mathbb{R}^3\) es una composición de movimientos rígidos, inversiones y homotecias.

Usando este hecho y algo de geometría diferencial, demostramos³ el siguiente teorema:

Teorema 2. Sea \(S\) una superficie orientable, compacta y regular y \(\Phi:S\to\mathbb{R}^3\) una transformación conforme e inyectiva. Entonces \S’=\Phi(S)\ es también una superficie orientable, compacta y regular y el funcional de Willmore es invariante bajo transformaciones conformes, es decir, \(W(S)=W(S’)\).

Primera fórmula de variación del funcional de Willmore

En el último capítulo, estudiamos la primera variación del funcional de Willmore. Los métodos variacionales son una herramienta muy poderosa en geometría, ya que nos permiten encontrar puntos críticos de un funcional estudiando el comportamiento del funcional cuando la superficie se perturba ligeramente.

Después de muchas (¡muchas!) cuentas, derivamos la siguiente fórmula para la primera variación del funcional de Willmore: \[w’(0)=\int_R\varphi(\Delta H+2H(H^2-2K))dS,\] donde \(\varphi\) es la función de escala de la variación normal de la superficie y \(R\) es la región encerrada por la superficie en la que la variación está definida con soporte compacto, es decir, \(\varphi=0\) fuera de \(R\). Además, \(H\) y \(K\) son las curvaturas media y gaussiana de la superficie, respectivamente, y \(\Delta\) es el operador laplaciano. Finalmente, \(w(t)\) es el funcional de Willmore de la superficie \(S_t\) obtenida al perturbar la superficie \(S\) en la dirección del campo vectorial normal \(\nu\) con función de escala \(\varphi\), es decir, \(S_t=S+t\varphi\nu\).

If the previous paragraph is a bit obscure to you, don’t worry! The important thing is that we derived a formula that every critical point of the Willmore functional must satisfy. With this formula, we were able to derive the Euler-Lagrange equation of the Willmore functional, which is a partial differential equation that every critical point of the Willmore functional must satisfy:

Teorema 3. Sea \(S\) una superficie regular. Entonces, \(S\) es un punto crítico del funcional de Willmore si y sólo si satisface la siguiente ecuación en derivadas parciales: \[\Delta H+2H(H^2-2K)=0.\]

Nótese que hemos eliminado el adjetivo ‘compacta’ del teorema anterior. Esto es porque este teorema nos permite redefinir el concepto de superficie de Willmore a todo el espacio de superficies regulares, no sólo a las compactas. Este es un resultado muy importante, ya que nos permite estudiar el funcional de Willmore en un contexto más general.

Gracias a este teorema, pudimos probar los siguientes resultados:

Teorema 4. Las superficies totalmente umbilicales son superficies de Willmore.

Las superficies totalmente umbilicales verifican \(H^2-K=0\), por lo que la parte derecha de la ecuación es cero. El término \(\Delta H\) también es cero, ya que \(H\) es constante. Por lo tanto, la ecuación se satisface.

Corolario. Los planos son superficies de Willmore bajo la nueva definición, pero no bajo la antigua, ya que no son compactos.

Teorema 5. Los trozos de esfera son las únicas superficies de Willmore con curvatura media constante no nula.

Supongamos que \(S\) es una superficie de Willmore con \(H\neq0\), entonces \(\Delta H = 0\) y la ecuación se convierte en \(H(H^2-2K)=0\). Como \(H\neq0\), tenemos que \(H^2-2K=0\), por lo que \(S\) es totalmente umbilical. Por lo tanto, \(S\) es un trozo de esfera ya que \(H\neq0\).

References

1. T. J. Willmore, Note on embedded surfaces, An. St. Univ. Iasi 11 (1965), 493-496. ↩

2. F. C. Marques and A. Neves, Min-max theory and the Willmore conjecture, Ann. of Math. (2) 179 (2014), no. 2, 683-782. arXiv ↩ ↩²

3. Para más detalles, puede consultar mi TFG. ↩ ↩²

4. Mirjam Soeten. Conformal maps and the theorem of Liouville. Bachelor’s Thesis, Rijksuniversiteit Groningen, 2013. link ↩