Perceptron: preludio de las redes neuronales

Introducción

We have all heard about neural networks, and how they are somehow a model of the human brain. Usually, this topic is presented as a black box, where we input some data, and we get some output. But, how does it work? What is the math behind it?

In this post I will try to explain what a perceptron is, both in plain words and in math. We will see how it works, and how it can be used to solve some problems. We will also see how it is related to neural networks. Finally, we will implement a perceptron from scratch in MATLAB.

Todos hemos oído hablar de las redes neuronales, y de cómo son de alguna manera un modelo del cerebro humano. Normalmente, este tema se presenta como una caja negra, donde introducimos algunos datos, y obtenemos una salida. Pero, ¿cómo funciona? ¿Cuál es la matemática detrás de esto?

En este post intentaré explicar qué es un perceptrón, tanto intuitivamente como matemáticamente. Veremos cómo funciona, y cómo se puede utilizar para resolver algunos problemas. También veremos cómo está relacionado con las redes neuronales. Finalmente, implementaremos un perceptrón desde cero en MATLAB.

¿Qué es un perceptrón?

Tratando de comprender el comportamiento del cerebro humano, McCulloch y Pitts propusieron en 1943 un modelo de neurona, que llamaron perceptrón¹, más tarde conocido como neurona de McCulloch-Pitts. Este modelo es una versión simplificada de una neurona real, que entendieron como una compuerta lógica binaria.

Vamos a desglosar esto un poco. No soy un biólogo, así que perdonadme si no soy lo suficientemente preciso en esta parte. Todos sabemos más o menos que hay 5 sentidos en nuestro cuerpo, que básicamente recopilan información de nuestro entorno. Esta información se envía al cerebro, donde se procesa de alguna manera, produciendo una respuesta. Esta respuesta se envía a diferentes partes del cuerpo, produciendo efectivamente una acción, que puede ser consciente (mover la mano) o inconsciente (respirar). El principal misterio es cómo se logra ese procesamiento. Ramón y Cajal descubrió² que el cerebro está formado por células, a las que llamó neuronas. Estas neuronas están conectadas entre sí, y son las que procesan la información. La información puede enviarse de una neurona a otra a través de una sinapsis, que es básicamente una conexión entre dos neuronas. Cuando una neurona recibe suficiente información, esta ‘dispara’, enviando señales a todas las neuronas a las que está conectada. Esta es la idea básica de una neurona y lo que McCulloch y Pitts intentaron modelar.

Aquí podemos ver un diagrama de una neurona:

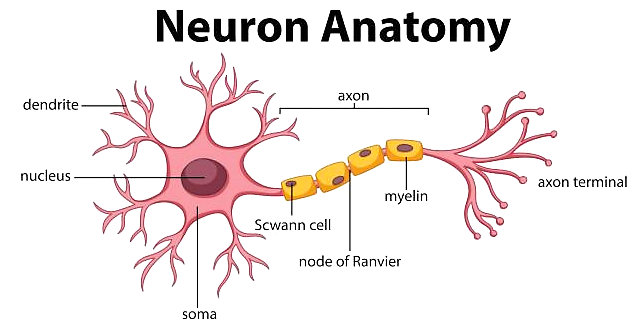
La neurona recibe información de otras neuronas a través de las dendritas. Esta información se procesa en el soma, y si es suficiente, dispara a través del axón, enviando señales a otras neuronas a través de las sinapsis, que son las uniones entre las terminales del axón y las dendritas de otras neuronas.

Por lo tanto, la neurona se puede ver como una compuerta lógica binaria, que recibe entradas y produce una salida o no. Matemáticamente, esto se escribe como una función \[f:\mathbb{R}^n\rightarrow\{0,1\}\] donde \(n\) es el número de entradas, y \(f\) es la función de activación. Esta función se puede definir de diferentes maneras, pero la más intuitiva es realizar primero una suma ponderada de las entradas, y luego aplicar una función de umbral al resultado. Este enfoque es intuitivo porque la suma ponderada captura la idea de que la neurona está conectada a otras neuronas, con diferentes niveles de importancia, y la función de umbral captura la idea de que la neurona dispara o no. Por lo tanto, la función de activación se puede escribir como \[f(x)=\begin{cases}1&\text{if }w^Tx+b>0\\0&\text{otherwise}\end{cases}\] donde \(x\in\mathbb{R}^n\) es la entrada, \(w\in\mathbb{R}^n\) es el vector de pesos, y \(b\in\mathbb{R}\) es el sesgo. El sesgo se puede ver como el umbral de la neurona, y el vector de pesos como la importancia de cada entrada.

Una representación visual de esta función se puede ver en la siguiente figura:

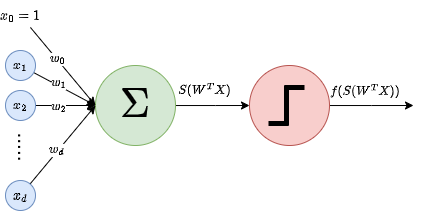
Como podemos ver, los inputs se multiplican por los pesos, y luego se suman al sesgo. Si el resultado es mayor que cero, la neurona dispara, de lo contrario no lo hace. Hay que tener en cuenta que esto es equivalente a un clasificador lineal, que separa el espacio de entrada en dos regiones, una para cada clase. Esto se debe a que la función es lineal en la entrada, y por lo tanto la frontera de decisión es un hiperplano.

Encontrando los pesos y el umbral

Ahora bien, ¿cómo sabemos los valores de \(w\) y \(b\)? Bueno, esta es la parte complicada. No podemos simplemente preguntarle a la neurona cuáles son los valores de \(w\) y \(b\), porque no lo sabe. Tenemos que encontrarlos nosotros mismos. Esto se hace entrenando la neurona. La idea es darle a la neurona algunas entradas para las que sabemos cuál debería ser la salida, y luego ajustar los valores de \(w\) y \(b\) para que la salida de la neurona sea la esperada. Esto se hace utilizando una función de pérdida, que mide qué tan lejos está la salida de la neurona de la salida esperada. La función de pérdida generalmente se define como el error cuadrático entre la salida esperada y la salida real, es decir, \[L(w,b)=(y-f(x))^2,\] donde \(y\) es la salida esperada. La idea es minimizar esta función de pérdida, de modo que la salida de la neurona esté lo más cerca posible de la salida esperada. Para minimizar este valor, podemos intentar tomar la derivada de la función de pérdida y luego establecerla en cero. Sin embargo, esto no es posible, porque la función de pérdida no es diferenciable.

Por lo tanto, un enfoque común es cambiar la función de activación a una diferenciable, como la función sigmoide, que se define como \[\sigma(x)=\frac{1}{1+e^{-x}}.\] Esta función es diferenciable, y se encuentra entre 0 y 1, de modo que se puede interpretar como una probabilidad de que la neurona dispare, en lugar de una salida binaria. Esto hace que el modelo sea más flexible, así como interpretable como una distribución de probabilidad, donde la variable de salida es una variable aleatoria de Bernoulli, \(y\sim Ber(\sigma(w^Tx+b))\). Este es el enfoque que seguiremos en este post. También podemos embeber el sesgo en el vector de pesos, agregando un 1 al vector de entrada, de modo que la función del perceptrón se pueda escribir como \[f(x)=\sigma(w^Tx).\] Ahora, en lugar de hablar directamente sobre el error, es más común hablar sobre la verosimilitud del modelo estimado, que básicamente nos dice cómo de probable es que el modelo produzca los datos observados. La función de verosimilitud se define como \[\mathcal{L}(W)=\prod_{i=1}^m\sigma(w^Tx_i)^{y_i}(1-\sigma(w^Tx_i))^{1-y_i},\] donde \(w={w_1,\dots,w_n}\) es el conjunto de pesos, \(x_i\) es la entrada \(i\)-ésima, e \(y_i\) es la salida \(i\)-ésima. La idea es maximizar esta función, de modo que el modelo tenga más probabilidades de producir los datos observados. Esto es equivalente a minimizar el logaritmo negativo de la verosimilitud, que se define como \[-\log\mathcal{L}(W)=-\sum_{i=1}^m\left[y_i\log\sigma(w^Tx_i)+(1-y_i)\log(1-\sigma(w^Tx_i))\right].\] Esta función se llama función de pérdida de entropía cruzada, y es la que usaremos para entrenar nuestro perceptrón.

Al diferenciarlo³, se obtiene (después de algunos cálculos): \[\nabla E(W)=\frac{\partial E(W)}{\partial W}=\sum_i[\sigma(w^Tx_i)-y_i]x_i.\] Desafortunadamente, esta ecuación no tiene una solución de forma cerrada, por lo que tenemos que usar un método iterativo para encontrar los pesos. El método más común es el descenso de gradiente, pero también se pueden usar otros métodos como el método de Newton.

Descenso de gradiente

El método de descenso de gradiente es un método numérico general para encontrar mínimos locales de una función diferenciable \(F(w)\). La idea es usar el hecho de que el gradiente de una función vectorial apunta en la dirección de máximo crecimiento, y el gradiente negativo apunta en la dirección de máximo decrecimiento. Por lo tanto, si ’seguimos’ esta dirección, deberíamos acercarnos a un mínimo de la función, aunque podría no ser el mínimo global. El enfoque funciona de la siguiente manera. Para aproximar un mínimo local de \(F(W)\):

1. Inicializar \(W_0\) a algún valor aleatorio. Establecer \(k=0\).
2. Calcular el gradiente de \(F(W)\) en \(W_k\), \(\nabla F(W_k)\).
3. Actualizar \(W_k\) a \(W_{k+1}=W_k-\gamma\nabla F(W_k)\), donde \(\gamma\) es la tasa de aprendizaje, y cuantifica ’cuánto’ avanzamos en la dirección del gradiente. Tiene que ser elegido de antemano y es crítico, ya que:
   • Si \(\gamma\) es demasiado pequeño, el algoritmo tardará demasiado en converger.
   • Si \(\gamma\) es demasiado grande, podríamos saltar sobre el mínimo y el método podría no converger nunca. Relacionado con la tasa de aprendizaje está la importancia de la escala de las variables, ya que la misma tasa de aprendizaje impacta a todas las características, por lo que si estas tienen diferentes escalas, el método podría ser bueno para algunas de ellas, pero malo para otras.
4. Repetir los pasos 2 y 3 hasta alcanzar convergencia.

Método de Newton

El método de Newton⁴ es un algoritmo utilizado para encontrar raíces de una función que converge más rápido que el descenso de gradiente y no necesita de la tasa de aprendizaje. Como este algoritmo encuentra raíces (es decir, ceros), no lo aplicamos directamente a \(F\), sino a su gradiente. Por lo tanto, en este caso, necesitamos que \(F\) sea dos veces diferenciable y que pueda permitirse calcular sus segundas derivadas, que a veces pueden ser costosas. En este caso, el algoritmo funciona de la siguiente manera:

1. Inicializar \(W_0\) a algún valor aleatorio. Establecer \(k=0\).
2. Calcular el Hessiano de \(F(W)\) en \(W_k\), \(H(F(W))=\nabla^2 F(W_k)\).
3. Actualizar \(W_k\) a \(W_{k+1}=W_k-H(F(W_k))^{-1}\nabla F(W_k)\).
4. Repetir los pasos 2 y 3 hasta alcanzar convergencia.

When we apply Newton’s method to the perceptron, we are doing what is called Iterated Reweighted Least Squares (IRLS), and the Hessian is: \[H(F(W))=\nabla^2 F(W_k)=X^T\cdot diag(\sigma(w^Tx_i)(1-\sigma(w^Tx_i)))\cdot X.\]

Cuando aplicamos el método de Newton al perceptrón, estamos haciendo lo que se llama Mínimos Cuadrados Iterados Ponderados (IRLS), y el Hessiano es: \[H(F(W))=\nabla^2 F(W_k)=X^T\cdot diag(\sigma(w^Tx_i)(1-\sigma(w^Tx_i)))\cdot X.\]

Entrenando el perceptrón

Así, para entrenar el perceptrón, le damos ejemplos \(X_i,y_i\) y aplicamos uno de estos métodos para actualizar los pesos, según el resultado obtenido, para cada ejemplo. Esto se llama aprendizaje en línea, y es el enfoque más común. El otro enfoque se llama aprendizaje por lotes, y consiste en aplicar el método a todo el conjunto de datos, en lugar de a cada ejemplo.

Implementación en MATLAB

Función de activación umbral

Vamos a comenzar con un ejemplo usando la función de activación umbral, y luego pasaremos a la función de activación sigmoide. El algoritmo de aprendizaje se basa en el descenso de gradiente, y puedes consultarlo en mis notas³ si estás interesado en los detalles.

Primero, generamos los datos que queremos clasificar. Queremos que el modelo sea capaz de clasificar los puntos como 1 si son mayores que 0.5, y como 0 en caso contrario. Usaremos el siguiente código para generar los datos:

rng(5)
X = rand([100,1]);
y = 2*(double(X>0.5)-0.5*ones(size(X)));

f=gscatter(X,zeros(size(X)),y,'br','o');
hold on
ylim([-0.1,0.1])
hold off

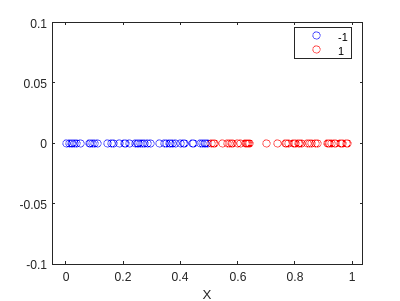
Ahora bien, este caso es bastante fácil, y podemos hacerlo a mano. Sabemos que el modelo es una línea, y podemos ver que la línea que separa las dos clases es \(x=0.5\). Por lo tanto, podemos definir los pesos como \(w=[-0.5,1]^T\).

W = [-0.5; 1]

W = 2x1    
   -0.5000
    1.0000

Si utilizamos este modelo para clasificar los datos, obtenemos el siguiente resultado:

% Add the bias
X_bias = [ones(size(X)) X];

pred = zeros(size(X));

for i=1:length(X)
    x = X_bias(i,:)';
    S = state(x,W);
    pred(i) = my_sign(S);
end

f2=gscatter(X,zeros(size(X)),pred,'br','o');
hold on
ylim([-0.1,0.1])
hold off

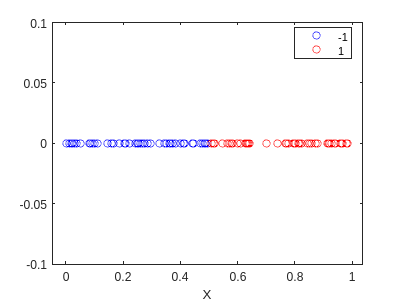
¡Ha hecho una clasificación perfecta! Ahora vamos a entrenar usando el algoritmo. Primero, tenemos que definir las funciones que necesitaremos:

function S = state(X, W)
    S = W'*X;
end

function pred = my_sign(S)
    if S > 0
        pred = 1;
    else
        pred = -1;
    end
end

function W = train(X, y, lr, epochs)
    [~, d] = size(X);
    W = zeros(d, 1);
    for epoch = 1:epochs
        for i = 1:length(X)
            x = X(i,:)';
            pred = my_sign(state(x, W));
            if pred ~= y(i)
                W = W + lr*x*y(i);
            end
        end
    end
end

Entonces, podemos entrenar el modelo:

% Add the bias
X_bias = [ones(size(X)) X];

% Train the model
W2 = train(X_bias,y,0.1,10)

W2 = 2x1    
   -0.1000
    0.2013

pred2 = zeros(size(X_bias));

for i=1:length(X)
    x = X_bias(i,:)';
    S = state(x,W2);
    pred2(i) = my_sign(S);
end

f3=gscatter(X,zeros(size(X)),pred2,'br','o');
hold on
ylim([-0.1,0.1])
hold off

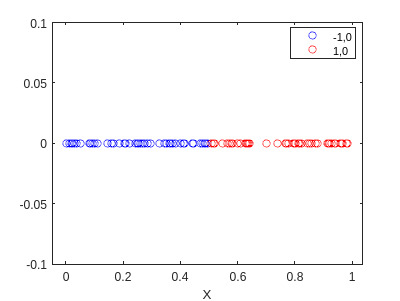
Esto es muy interesante… encontró diferentes pesos, pero clasificó todo bien. Esto debe romperse en algún lugar. Intentemos determinar dónde:

X = 0.45:0.001:0.55;
X = X';
y = 2*(double(X>0.5)-0.5*ones(size(X)));

X_bias = [ones(size(X)) X];

pred3 = zeros(size(X));

for i=1:length(X)
    x = X_bias(i,:)';
    S = state(x,W2);
    pred3(i) = my_sign(S);
end

f4=gscatter(X_bias,zeros(size(X)),pred3==y,'br','o');
hold on
ylim([-0.1,0.1])
xlim([0.45,0.55])
hold off

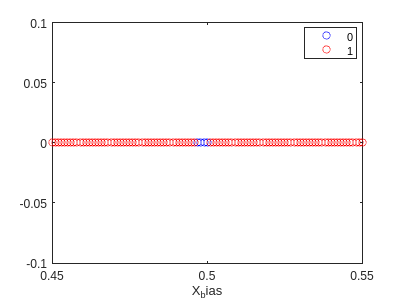
y(pred3~=y)

ans = 4x1    
    -1
    -1
    -1
    -1

Esto significa que nuestro modelo está estableciendo el límite un poco antes de 0.5 (como se puede ver en el gráfico). Esto debería mejorarse aumentando el tamaño de X.

Función de activación sigmoide

En este caso, utilizaremos un conjunto de datos un poco más complejo. Generaremos los datos utilizando el siguiente código:

rng(5)
X1 = rand([100,1])*2.+1;
X2 = rand([100,1])*3.;
y = double(X2>X1.*1.5-1);

X = [X1 X2];

f=gscatter(X1,X2,y,'br','o');
hold on
plot(X1,X1.*1.5-1,'g')
legend('0','1','Real separation','Location','northoutside')
hold off

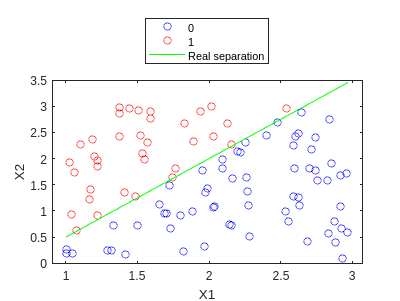
Y ahora entrenamos usando el descenso de gradiente. De nuevo, definimos nuestras funciones de entrenamiento:

function S = state(X, W)
    S = X*W;
end

function s=logistic(S)
    s = 1./(1+exp(-S));
end

function ds=grad_logistic(y, y_hat, X)
    ds = X' * (y_hat - y);
end

function H = hess_logistic(y_hat, X)
    D = diag(y_hat .* (1 - y_hat));
    H = X' * D * X;
end

function [W,niter]=train_GD(X, y, lr, threshold, maxiter)
    [~, d] = size(X);
    W = ones(d, 1);
    for niter=1:maxiter
        st = state(X,W);
        y_hat = logistic(st);
        ds = grad_logistic(y, y_hat, X);
        v = vecnorm(abs(ds));
        if v < threshold
            break
        end
        W = W - lr*ds;
    end
end

function [W, niter] = train_NR(X, y, threshold, maxiter, lambda)
    [~, d] = size(X);
    W = ones(d, 1);
    I = eye(d);
    for niter = 1:maxiter
        st = state(X, W);
        y_hat = logistic(st);
        gradient = grad_logistic(y, y_hat, X);
        v = vecnorm(abs(gradient));
        if v < threshold
            break
        end
        H = hess_logistic(y_hat, X);
        W = W - inv(H + lambda * I) * gradient; %We add a term to avoid singularities
    end
end

function pred = my_predict(X, W)
    p = logistic(state(X, W));
    pred = double(p >= 0.5);
end

Ahora podemos entrenar el modelo:

[n, d] = size(X);
X_bias = [ones(n,1) X]; # Add the bias

[W,niter] = train_GD(X_bias,y,0.1,1e-3,20) #Train the model with learning rate 0.1, tolerance 1e-3 and 20 iterations

W = 3x1    
    3.9647
  -13.2924
   13.2435

niter = 20

Y hacemos la predicción:

y_hat = my_predict(X_bias,W);

f2=gscatter(X1,X2,y_hat,'br','o');
hold on
plot(X1,X1.*1.5-1,'g')
legend('0','1','Real separation','Location','northoutside')
hold off

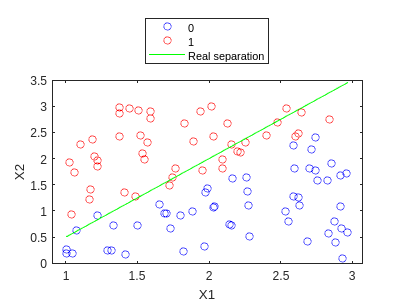
Vemos que es bastante bueno… Incrementemos el parámetro max_iter:

[W,niter] = train_GD(X_bias,y,0.1,1e-3,1000)

W = 3x1    
   20.9642
  -27.7530
   17.3205

niter = 1000

y_hat = my_predict(X_bias,W);

f3=gscatter(X1,X2,y_hat,'br','o');
hold on
plot(X1,X1.*1.5-1,'g')
legend('0','1','Real separation','Location','northoutside')
hold off

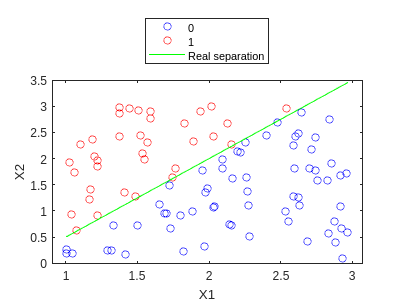
Y de hecho es mucho mejor! :D

Veamos qué tal funciona IRLS:

[W,niter_NR] = train_NR(X_bias,y,1e-3,1000,1e-3)

W = 3x1    
1.0e+05 *

    1.6554
   -2.0991
    1.2912

niter_NR = 227

y_hat = my_predict(X_bias,W);

f4=gscatter(X1,X2,y_hat,'br','o');
hold on
plot(X1,X1.*1.5-1,'g')
legend('0','1','Real separation','Location','northoutside')
hold off

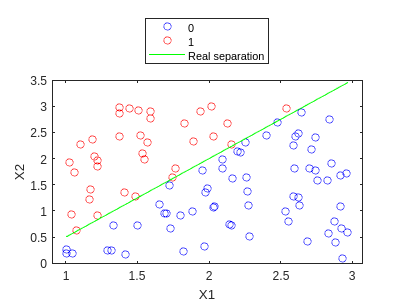
We can see how this time we also obtain nice separation, and this one even finishes before maxiter is reached. In fact, we can try to see how many iterations would GD need:

Observamos que esta vez también obtenemos una buena separación, y ahora incluso termina antes de que se alcance maxiter. De hecho, podemos ver cuántas iteraciones necesitaría GD:

[W,niter_GD] = train_GD(X_bias,y,0.1,1e-3,1000000)

W = 3x1    
  110.2037
 -146.6376
   92.3106

niter_GD = 449262

Por tanto, obtenemos un speedup enorme:

speedup = niter_GD / niter_NR

speedup = 1.9791e+03

Casi 2000 veces más rápido en términos de iteraciones…

Conclusiones

En este post hemos entendido los conceptos básicos del perceptrón, y cómo es útil para clasificar datos. Hemos visto varios métodos para entrenarlo en el caso simple de clasificación binaria, y hemos visto cómo IRLS necesitaba muchas menos iteraciones que GD para converger. No obstante, calcular el Hessiano puede ser bastante caro, y encontrar su inversa no siempre es posible.

Hemos visto cómo implementar el perceptrón en Matlab, y cómo entrenarlo usando GD y IRLS, y aunque los ejemplos proporcionados parecen fáciles, puedes cambiar los datos a cualquier problema de clasificación binaria que quieras y funcionará (ten en cuenta que estos algoritmos no están tan optimizados como los de Matlab, por lo que serán más lentos, pero funcionarán).

Espero que hayas aprendido algo nuevo, y si tienes alguna pregunta, ¡no dudes en preguntarme! En los siguientes posts veremos cómo extender el perceptrón a la clasificación multiclase, y cómo usarlo para resolver problemas de regresión. Entonces, estaremos listos para ver cómo los perceptrones se pueden usar para crear redes neuronales, y cómo entrenarlas usando el método de backpropagation.

¡Nos vemos en el siguiente post!

References

1. McCulloch, W. S., & Pitts, W. (1943). A logical calculus of the ideas immanent in nervous activity. The bulletin of mathematical biophysics, 5, 115-133. ↩

2. Ramón y Cajal, S. (1894). The croonian lecture: La fine structure des centres nerveux. Proceedings of the Royal Society of London, 55, 444-468. ↩

3. You can check my notes on Machine Learning, UPC ↩ ↩²

4. There is an infinite amount of Newton’s algorithms haha, this is one of them :D ↩